fenómenos matemáticos

 Quizá no es perceptible a simple vista, pero las matemáticas están presentes en cada ámbito de nuestras vidas. Aunque a muchos produzca dolor de cabeza pensar en ecuaciones, figuras geométricas y polinomios es imposible negar la belleza manifiesta en la simetría de la naturaleza o en los objetos creados por el hombre.

“Las matemáticas no sólo se ven bellas, pues la belleza también es matemática. Ambas están interconectadas”, señala Thomas Britz, un matemático de la Universidad de Nueva Gales del Sur, en Australia. Britz se especializó en combinatoria, una rama de las matemáticas dedicada al conteo complejo y la resolución de rompecabezas, aunque también suele abordar cuestiones filosóficas de esta ciencia exacta.

En 2008, durante una TedTalk titulada “Las emociones de las matemáticas”, el profesor abordó la forma en que las matemáticas están vinculadas directamente con las emociones humanas, incluida la belleza.

“Nuestros cerebros nos recompensan al reconocer patrones, ya sea observando simetrías, organizando partes de un todo y resolviendo rompecabezas”, dijo Britz. “Si llegamos a identificar algo que se desvía del patrón, cuando aparece un suceso inesperado, nuestros cerebros nos vuelven a recompensar. Experimentamos alegría y entusiasmo”.

Irregularidad y simetría.

El experto dice que el concepto de simetría se considera bello entre los humanos, aunque la irregularidad en los patrones también nos resulta interesante. Por ejemplo, la belleza humana ha sido ampliamente vinculada con rostros simétricos. Sin embargo, las características que interrumpen ligeramente ese patrón aportan a la belleza.

En muchos conceptos matemáticos se encuentran dinámicas semejantes entre patrones e irregularidades, elegancia y caos, verdad y misterio. “Es lo mismo que observamos en la música”, dice Britz. “Los sonidos estandarizados y ordenados con un toque espontáneo agregan personalidad, elegancia y profundidad”.

Los fractales.

Definidos de la forma más simple, los fractales son patrones autorreferenciales que se repiten en pequeñas escalas, hasta cierto límite. Dicho de otra forma: entre más de cerca analicemos un fractal, mayor será el número de repeticiones que logremos observar.

Esta repetición de patrones está presente en una variedad de fenómenos y seres vivos. La naturaleza se ha encaprichado con los fractales a través de los copos de nieve, flores, árboles, rutas pluviales, el sitio de impacto de los rayos en incluso los vasos sanguíneos. Sin embargo, en la naturaleza los fractales están limitados a unas cuantas repeticiones.

Pero, en el mundo de las matemáticas teóricas los fractales pueden repetirse indefinidamente. Britz dice que los fractales artificiales pueden analizarse, pero jamás llegaríamos a su fin. “Los fractales son infinitamente profundos”, agrega el experto.

Constante Pi.

¿Qué es lo primero que piensas cuando escuchas el número Pi? En el ámbito matemático es imprescindible cuando se trata de círculos, pero la constante va mucho más allá. Britz asegura que Pi está presente en muchos sitios de la naturaleza o en fórmulas matemáticas ajenas a las circunferencias.

Aunque sabemos cómo empieza (3.14), Pi es un número infinito. Desafortunadamente, entre todos los decimales conocidos de este número (50 billones de dígitos) los matemáticos no han encontrado un solo patrón. El gran misterio que oculta Pi ha imposibilitado a los expertos determinar con exactitud la circunferencia o área de un círculo.

“¿Qué sucede en este caso? ¿Qué es este extraño número que, de alguna forma, vincula a todos los círculos?”, se pregunta Britz. “Existe algún misterio oculto en Pi, pero no lo comprendemos. Ese aspecto místico sobre la constante hace que todo sea más bello”.

La proporción áurea.

Seguramente has escuchado sobre esto, pues desde hace algunas décadas se integró a la cultura popular. Según Britz, la proporción áurea es la forma estética más agradable que podemos encontrar en un objeto. Su equivalencia aproximada es de 1.618 y puede representarse geométricamente con la Espiral Dorada.

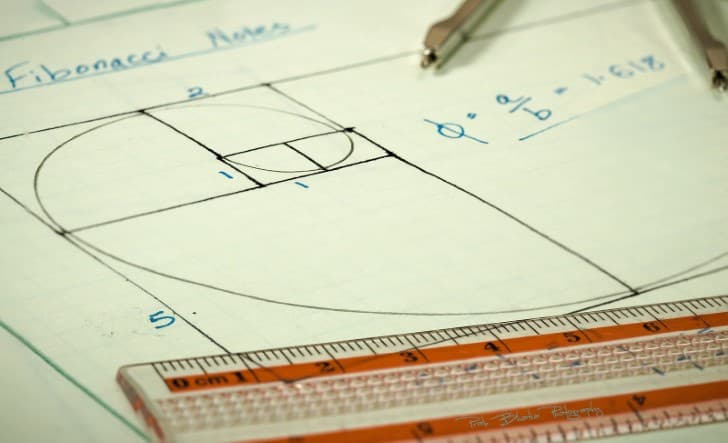
La proporción áurea está presente en la naturaleza y nos ha acompañado desde hace mucho tiempo. Artistas, diseñadores y fotógrafos la han socorrido para intentar el trabajo perfecto. “A través de la historia, la proporción es tratada como una referencia a la forma ideal ya sea en el arte, la arquitectura o el propio cuerpo humano”, dice Britz. No por nada se le conoce como Proporción Divina.

Paradoja Banach-Tarski.

Si tienes una esfera en un espacio tridimensional y la divides en partes específicas, existe una forma de reordenar las partes para crear dos esferas. La oración anterior resumen a grandes rasgos un famoso teorema geométrico llamado paradoja Banach-Tarski. “Ya es interesante, pero se pone aún más extraño”, anotó Britz.

Y es que cuando estas esferas sean creadas, ambas tendrán el mismo tamaño que la primera. Aunque es imposible en el mundo físico, en el ámbito matemático el teorema funciona, y para el profesor esto es “algo mágico”.

“Se requiere de mucho conocimiento previo para experimentar las partes bellas de las matemáticas. Un entrenamiento básico que para muchos es aburrido. Pero vale la pena. Tengo la esperanza de que más personas lleguen a esa parte divertida de las matemáticas. Aún existe mucha belleza por descubrir”, finaliza el profesor.

A continuación encontrarás la TedTalk ofrecida por Britz el año pasado. Desafortunadamente no tiene subtítulos en español.